Base d'épreuves orales scientifiques de concours aux grandes écoles

Énoncé(s) donné(s)

Certaines montres ne possèdent pas de piles et se rechargent grâce aux mouvements du poignet qui font tourner un balancier.Ce balancier est une section de disque, d'épaisseur constante.

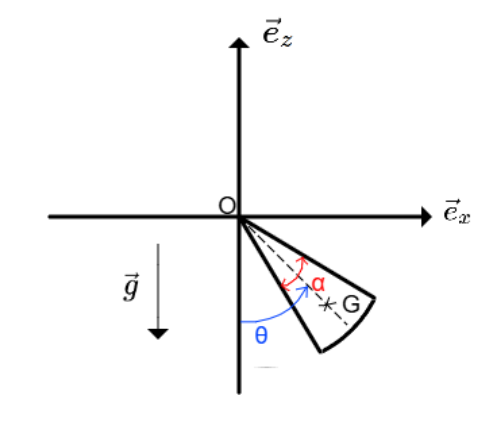
On donne sa masse : $m$, son angle d'ouverture $\alpha$, son moment d'inertie en O par rapport à $\vec{y}$  : $J=\frac{1}{{2}}mR^{2}$ et la distance de O au centre de masse : $d=OG=R\frac{\sin\left(\frac43\alpha\right)}{{3}\alpha}$. On modélise l'accéleration transmise par le poignet en O par $\vec{a}=a(t)\vec{e}_{x}$

1)Le référentiel attaché à O est il galiléen ?

2)Expliquer pourquoi $d$ dépend de $\alpha$

3)Déterminer l'équation différentiel vérifiée par $\theta$

4)En supposant que l'angle du balancier reste modérée et que $\vert\theta\vert<<\frac{\lvert a\left(t\right)\rvert}{g}$ simplifier cette équation différentielle

On considère maintenant $a(t)$ constant pendant une durée $\tau$

5)Déterminer l'énergie cinétique maximale du balancier

6)A l'aide du code python montrer qu'il existe une valeur de $\alpha$  maximisant cette énergie cinétique

7)Quelle(s) condition(s) $\tau$ doit il respecter pour valider ce modèle ?

8)Discuter de possibilités d'amélioration du modèle de $a(t)$

Indication(s) fournie(s) par l'examinateur pendant l'épreuve

Commentaires divers

-Le code python (que je n'ai pas eu à modifier) donné un graphique de l'énergie cinétique maximale en fonction de l'angle $\alpha$

• schéma exo pendule .png