Énoncé(s) donné(s)
Exercice 1 :
On considère un sol à l'altitude z > 0, en contact avec l'atmosphère en z = 0. On cherche à visualiser les variations de température $T = T(z,t)$ au sein de ce sol. On donne $T(0, t) = T_{0} + cos(wt)$.
Enfin on pose $\theta(z,t) = T(z,t) - T_{0}$
1) On cherche $\theta$ sous la forme $\underline{\theta}(z,t) = \underline{f}(z)e^{iwt}$. Déterminer $T(z,t)$
Exercice 2 :
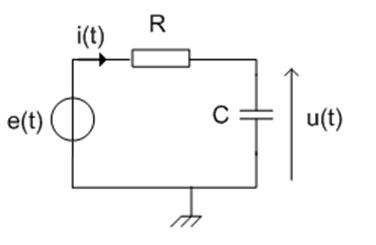
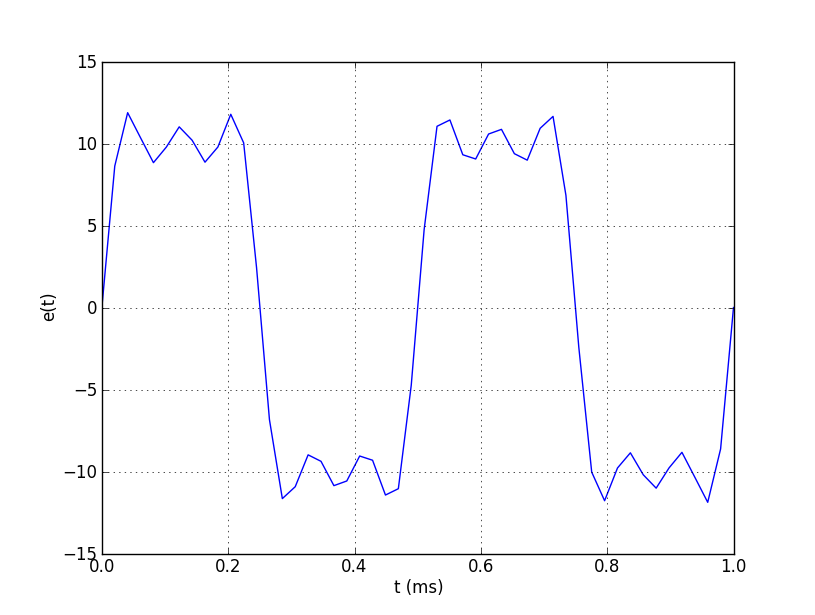
On considère un circuit RC comme décrit ci-dessus. On donne $e(t) = 10\frac{4}{\pi}(sin(wt) + \frac{1}{3}sin(3wt) + \frac{1}{5}sin(5wt))$
On donne de plus $R = 10 k\Omega$ et $C = 100 nF$
1) De quel type de filtre s'agit-il ? Donner sa caractéristique.
2) Déterminer approximativement $u(t)$, en tenant compte des données et des approximations que l'on peut faire.
Indication(s) fournie(s) par l'examinateur pendant l'épreuve
Commentaires divers
Examinateur fort sympathique, bien que peu bavard, et qui m'a laissé prendre de nombreuses iniatives.




Aucun commentaire posté pour le moment